| Definitions | P  Q, L1 Q, L1  L2, Id, f(a), x << y, #$n, ||as||, (x L2, Id, f(a), x << y, #$n, ||as||, (x  l), {i..j l), {i..j }, e c }, e c e', e e', e   X, E, X, E,   x. t(x), x. t(x),  x.A(x), pred(e), <a, b>, x.A(x), pred(e), <a, b>,  A, first(e), suptype(S; T), S A, first(e), suptype(S; T), S  T, T, 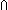 x:A.B(x), !Void(), x:A.B(x), !Void(),   x,y. t(x;y), pred!(e;e'), x,y. t(x;y), pred!(e;e'),  , SWellFounded(R(x;y)), constant_function(f;A;B), e < e', r , SWellFounded(R(x;y)), constant_function(f;A;B), e < e', r  s, val-axiom(E;V;M;info;pred?;init;Trans;Choose;Send;val;time), s, val-axiom(E;V;M;info;pred?;init;Trans;Choose;Send;val;time),  , Msg(M), kind(e), loc(e), Knd, kindcase(k; a.f(a); l,t.g(l;t) ), EOrderAxioms(E; pred?; info), IdLnk, Unit, EqDecider(T), strong-subtype(A;B), , Msg(M), kind(e), loc(e), Knd, kindcase(k; a.f(a); l,t.g(l;t) ), EOrderAxioms(E; pred?; info), IdLnk, Unit, EqDecider(T), strong-subtype(A;B), 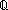 , a:A fp , a:A fp B(a), EState(T), type List, sys-antecedent(es;Sys), Top, B(a), EState(T), type List, sys-antecedent(es;Sys), Top,  , AbsInterface(A), Type, ES, , AbsInterface(A), Type, ES,  x:A. B(x), {x:A| B(x)} , Atom$n, chain-consistent(f;chain), hd(l), x:A. B(x), {x:A| B(x)} , Atom$n, chain-consistent(f;chain), hd(l),  b, adjacent(T;L;x;y), s = t, P b, adjacent(T;L;x;y), s = t, P   Q, no_repeats(T;l), a < b, P & Q, x:A Q, no_repeats(T;l), a < b, P & Q, x:A  B(x), B(x),  x:A. B(x), x:A x:A. B(x), x:A  B(x), E(X), x before y B(x), E(X), x before y  l, t l, t  T, left + right, {T}, increasing(f;k) T, left + right, {T}, increasing(f;k) |